MECÂNICA GRACELI GENER. - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [800]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES E CAMPOS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

O efeito Unruh, descoberto em 1976 por Bill Unruh da Universidade da Colúmbia Britânica, é uma previsão da teoria quântica de campos, de que um observador acelerado irá perceber um banho térmico, semelhante à radiação de corpo negro, enquanto um outro observador em repouso inercial não irá observar nenhum. Em outras palavras, o observador acelerado vai se encontrar em um ambiente mais aquecido. O estado quântico que é visto como um estado estático pelo observador inercial, é visto como um equilíbrio termodinâmico pelo observador uniformemente acelerado.

Teoria

Unruh demonstrou que mesmo a noção de vácuo depende do caminho que o observador percorre pelo espaço-tempo. Do ponto de vista do observador acelerado, o vácuo do observador inercial vai se assemelhar a um estado contendo várias partículas em um equilíbrio térmico – um gás aquecido. Apesar do Efeito Unruh parecer não intuitivo, faz perfeito sentido se a idéia de vácuo for corretamente interpretada.

Na física moderna o conceito de vácuo não é o mesmo que "espaço-vazio", como tudo mais no espaço é preenchido por campos quânticos que formam o universo. O vácuo é simplesmente o menor estado de energia possível deste campo.

Segundo a teoria da relatividade restrita, dois observadores se movendo relativamente em sentidos opostos devem utilizar diferentes coordenadas de tempo. Se estes observadores estiverem acelerados eles também deverão utilizar diferentes coordenadas espaciais. Cada um dos observadores irá enxergar diferentes estados quânticos e diferentes vácuos.

Em alguns casos, o vácuo de um observador não é sequer no espaço do espaço quântico do outro observador. Em termos técnicos, isto é por causa dos dois vácuos levarem a representações completamente diferentes do campo quântico.

A existência da radiação de Unruh pode ser referenciada para o horizonte de eventos, colocando-se no mesmo esboço conceitual da radiação Hawking. Por outro lado, o efeito Unruh mostra que a definição do que constitui uma partícula depende do estado inercial do observador.

O efeito Unruh é um mecanismo intrínseco da teoria quântica de campos, sendo necessário, por exemplo, para a obtenção correta do limite clássico de alguns fenômenos quânticos e a conexão desses fenômenos entre os pontos de vista de observadores inerciais e acelerados.^[1]^[2]^[3] Além disso, é necessário para explicar corretamente o próprio efeito Hawking e a consequente energia divergente percebida por um observador estático fora de um buraco negro.^[4]^[5]

Temperatura Unruh

A temperatura de Unruh é a temperatura efetiva experimentada por um detector uniformemente acelerado em um campo de vácuo, dada por:^[6]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

T={\frac {\hbar a}{2\pi ck_{\mathrm {B} }}},

onde $ħ$ é a constante de Planck reduzida, $a$ é a aceleração local, $c$ é a velocidade da luz, e $k B$ é a constante de Boltzmann. Dessa forma, por exemplo, uma aceleração própria de 2.47×10²⁰ m·s^-2 corresponde aproximadamente a uma temperatura de 1 K. Inversamente, uma aceleração de 1 m·s^-2 corresponde a uma temperatura de 4.06×10⁻²¹ K.^[7]

A temperatura de Unruh tem a mesma forma da temperatura de Hawking $T H = ħg 2π ck B$ para um buraco negro. Tal expressão foi obtida por Stephen Hawking de maneira independente por volta da mesma época. Por isso, tais equações são referenciadas também como Temperatura de Hawking–Unruh.^[8]

Energia do fotão ^{(português europeu)} ou energia do fóton ^{(português brasileiro)} é a energia carregada por um único fóton. A quantidade de energia está diretamente relacionada à frequência e ao comprimento de onda eletromagnética do fóton. Quanto maior for a frequência do fóton, maior a sua energia. Da mesma forma, quanto maior for o comprimento de onda do fóton, menor a sua energia.

A energia do fóton é uma função somente do comprimento de onda. Outros fatores, como intensidade da radiação, não afetam a energia do fóton. Em outras palavras, dois fótons de luz com a mesma cor e, portanto, o mesmo comprimento de onda, terão a mesma energia do fóton, mesmo se um for emitido por uma vela de cera e o outro for emitido pelo Sol.

A energia do fóton pode ser representada por qualquer unidade de energia. Umas das unidades mais comuns para denotar a energia do fóton é elétron-volt (eV) e joule (bem como seus múltiplos, como microjoule). Como um joule é igual a 6,24 × 10¹⁸ eV, as unidades maiores podem ser mais úteis para denotar a energia de fótons com frequências e energias mais altas, como o raio gama, ao contrário dos fótons de menor energia, como os da região do espectro eletromagnético de radiofrequência.

Se os fótons, de fato, não possuem massa, a energia do fóton não seria relacionada à massa através da equivalência E = mc². Os únicos dois tipos de tais partículas sem massa observados são os fótons e os glúons.^[1] Entretanto, o postulado de que os fótons não possuem massa é baseado na crise que resulta de outras teorias em mecânica quântica. Para que outras teorias, como a invariância de gauge e a chamada "renormalização" sobrevivam sem considerável revisão, os fótons devem permanecer sem massa no domínio das atuais equações.^[2] A alegação é contestada em outros meios.^[3] Diz-se que fótons possuem massa relativística (isto é, massa resultante do movimento de um corpo material em relação a outro). Além disso, algumas hipóteses propõem que toda massa ou "massa de repouso" pode ser composta de massa relativística acumulada, secundária ao movimento, uma vez que nenhum corpo material esteja ou possa estar em "repouso" em relação a todos os campos. Nessa hipótese, assim como o movimento se torna zero, a massa também se torna zero. Por outro lado, os fótons possuem movimento e energia variável em relação à frequência e ao comprimento de onda, sugerindo que várias formas do foton têm, cada uma, equivalência de massa diferente. Assim, a equação "E = mc²" mostraria que a massa e o movimento são conceitos indissociáveis e e fundamentalmente substituíveis para toda a matéria.^[4]

Fórmula

A equação para a energia do fóton^[5] é

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$E={\frac {hc}{\lambda }}$

Onde E é a energia do fóton, h é a constante de Planck, c é a velocidade da luz no vácuo e λ é o comprimento de onda do fóton. Como h e c são ambos constantes, a energia do fóton varia diretamente em relação ao comprimento de onda λ.

Para encontrar a energia do fóton em eV, usando o comprimento de onda em micrômetros, a equação é aproximadamente

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$E(eV)={\frac {1.2398}{\mathrm {\lambda } ({\mu }m)}}$

Portanto, a energia do fóton de comprimento de onda de 1 μm, próximo à da radiação infravermelho, é aproximadamente 1,2398 eV.

Como

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

////// ${\frac {c}{\lambda }}=f$ , onde f é a frequência, a equação da energia pode ser simplificada para

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$E=hf$

Esta equação é conhecida como a relação de Planck-Einstein. Substituindo h por seu valor em J⋅s e f por seu valor em hertz resulta na energia do fóton em joules. Portanto, a energia do fóton à frequência de 1 Hz é 6,62606957×10⁻³⁴ joules ou 4,135667516×10⁻¹⁵ eV.

Em química e engenharia óptica,

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$E=h{\nu }$

é usada onde h é a constante de Planck e a letra grega ν (ni) é a frequência do fóton.^[6]

A frequência (FO 1943: freqüência) é uma grandeza física que indica o número de ocorrências de um evento (ciclos, voltas, oscilações etc.) em um determinado intervalo de tempo.^[1] Alternativamente, podemos medir o tempo decorrido para uma oscilação. Esse tempo em particular recebe o nome de período (T). Desse modo, a frequência é o inverso do período. Por exemplo, se o coração de um bebê recém-nascido bate em uma frequência de 120 vezes por minuto, o seu período (intervalo entre os batimentos) é metade de um segundo.

Som
Onda
Amplitude
Fase
Frente de onda
Frequência fundamental
Harmônica
Frequência
Hertz
Altura tonal
Oitava
Velocidade do som
Efeito Doppler

Definições e unidades

Para processos cíclicos, tais como a rotação, oscilações, ou ondas, a frequência é definida como um número de ciclos por unidade de tempo. Em física e disciplinas de engenharia, tais como óptica, acústica e de rádio, a frequência é geralmente indicada por uma letra f Latina ou pela letra grega ν (nu). Note que a frequência angular é usualmente representada pela letra grega ω (ômega), que tem como unidade no SI radianos por segundo (rad/s).

Para contagens por unidade de tempo, a unidade no SI para a frequência é o hertz (Hz), em homenagem ao físico alemão Heinrich Hertz, 1 Hz significa que o evento se repete uma vez por segundo. Um nome anterior para esta unidade foi ciclos por segundo.

A unidade tradicional de medida utilizada com dispositivos mecânicos de rotação é rotações por minuto, RPM abreviado. 60 RPM equivalem a 1 hertz.

O período, normalmente indicado por T, é o período de tempo correspondente a um ciclo, e é o recíproco da frequência f:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

f={\frac {1}{T}}

A unidade no SI para o período é o segundo.

Medição

Por estroboscópio

Ver artigo principal: Estroboscópio

Um método mais velho de medição da frequência de rotação ou vibração de objetos é usar um estroboscópio.^[2] Este consiste em uma luz intensa repetitivamente intermitente (chamado strobe), cuja frequência pode ser ajustada com um circuito de temporização calibrado. A luz estroboscópica está apontada para o objeto de rotação e a frequência é ajustada para cima e para baixo. Quando a frequência do strobe é igual à frequência do objeto de rotação ou de vibração, o objeto completa um ciclo de oscilação e volta a sua posição original entre os flashes de luz, por isso, quando iluminado pelo strobe o objeto parece parado. Em seguida, a frequência pode ser lida a partir da leitura calibrada do estroboscópio. Uma desvantagem deste método é que um objeto girando a um múltiplo inteiro da frequência estroboscópica também parece estacionário.

Métodos heteródinos

Acima da faixa de contadores de frequência, as frequências de sinais eletromagnéticos geralmente são medidas indiretamente por meio do heteródino (conversão de frequência). Um sinal de referência com uma frequência conhecida perto da frequência desconhecida é misturado com a frequência desconhecida em um dispositivo de mistura não linear tal como um diodo. Isto cria um sinal heteródino,mais conhecido como "batimento", para a diferença entre as duas frequências. Se os dois sinais estão juntos em frequência, o heteródino é suficientemente baixo para ser medido por um contador de frequência. Este processo só mede a diferença entre a frequência desconhecida e a frequência de referência, que devem ser determinadas por qualquer outro método. Para chegar a frequências mais elevadas, várias fases do heteródino pode ser utilizado. A pesquisa atual está estendendo este método para frequências de infravermelho e de luz (detecção heteródina óptica).^[3]

Frequência das ondas

Para ondas periódicas, a frequência tem uma relação inversa com o conceito de comprimento de onda, simplesmente, a frequência é inversamente proporcional ao comprimento de onda λ (lambda). A frequência f é igual à velocidade de fase v da onda dividido pelo seu respectivo comprimento de onda λ:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

f={\frac {v}{\lambda }}

No caso especial de ondas electromagnéticas que se deslocam através do vácuo, temos, v = c, em que c é a velocidade da luz no vácuo, e esta expressão torna-se:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

f={\frac {c}{\lambda }}

Quando as ondas de uma fonte monocromática viajam de um meio para outro, a sua frequência permanece a mesma, apenas o seu comprimento de onda e velocidade mudam.

Luz

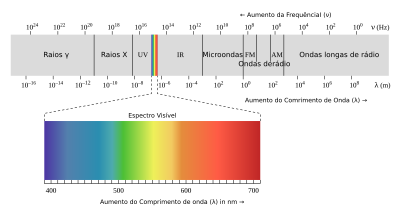
Ver artigos principais: Luz e Radiação eletromagnética

A luz visível é uma onda eletromagnética, composta de oscilações de campos elétricos e magnéticos que viajam através do espaço. A frequência da onda determina sua cor: 4×10¹⁴ Hz é a luz vermelha, 8×10¹⁴ Hz é a luz violeta, e entre essas frequências (na faixa de 4-8×10¹⁴ Hz) estão todas as outras cores do arco-íris. Uma onda electromagnética pode ter uma frequência inferior a 4×10¹⁴ Hz, mas será invisível ao olho humano, tais ondas são chamados de radiação infravermelha (IR). Para uma frequência menor, a onda é chamada de micro-ondas e em frequências mais baixas ainda é chamada de ondas de rádio. Do mesmo modo, uma onda eletromagnética pode ter uma frequência superior a 8×10¹⁴ Hz, mas será invisível ao olho humano e são chamadas de ondas de radiação ultravioleta (UV). Mesmo ondas de alta frequência são chamados de raios-X, e maior ainda de raios gama.^[4]

Todas essas ondas, começando com as ondas de rádio, de frequência menor, até os raios gama, de frequência mais elevada, são fundamentalmente a mesma, isto é, todas elas são chamadas de radiação eletromagnética. Elas viajam através do vácuo à velocidade da luz.

Outra propriedade de uma onda eletromagnética é o seu comprimento de onda. O comprimento de onda é inversamente proporcional à frequência, portanto, uma onda eletromagnética com uma frequência maior tem um comprimento de onda menor, e vice-versa.

Som

Ver artigo principal: Som

O som é constituído por alterações na pressão do ar sob a forma de ondas. As frequências que os ouvidos podem ouvir são limitadas a uma faixa específica de frequências.

Vibrações mecânicas são percebidas como viagens do som através de todas as formas de matéria: gases, líquidos, sólidos e plasmas. A matéria que apoia o som é chamada de meio de propagação, assim ele não pode viajar através do vácuo.

A gama de frequências audíveis para o ser humano é tipicamente dada como sendo entre cerca de 20 Hz e 20 000 Hz (20 kHz). As altas frequências, muitas vezes tornam-se mais difíceis de ouvir com a idade. Outras espécies têm diferentes gamas de audição. Por exemplo, algumas raças de cães podem perceber vibrações de até 60 000 Hz.^[5]

Frequências usadas em transmissões de televisão

As emissões de TV são feitas a partir da frequência 5 x 10⁷ Hz (50 MHz). É costume classificar as ondas de TV em bandas de frequência (faixa de frequência), que são:^[6]

VHF: very high frequency (54 MHz a 216 MHZ e canal 2 a 13)
UHF: ultra-high frequency (470 MHz a 890 MHz e canal 14 a 83)
SHF: super-high frequency
EHF: extremely high frequency
VHFI: very high frequency indeed

As ondas de TV não são refletidas pela ionosfera, de modo que para estas ondas serem captadas a distâncias superiores a 75 Km é necessário o uso de estações repetidoras.

Outros tipos de frequência

Frequência angular ω é definido como a taxa de variação do deslocamento angular, θ, (durante a rotação), ou a taxa de variação da fase da forma de onda senoidal (por exemplo, oscilações e ondas), ou como a taxa de alteração do argumento à função seno:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

y(t)=\sin \left(\theta (t)\right)=\sin(\omega t)=\sin(2\pi ft)

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\frac {d\theta }{dt}}=\omega =2\pi f

Frequência angular é normalmente medido em radianos por segundo (rad / s), mas, para os sinais de tempo discreto, pode também ser expressa como radianos por tempo de amostragem, que é uma quantidade adimensional. Frequência espacial é análoga à frequência temporal, mas o eixo do tempo é substituído por um ou mais eixos de deslocamento espacial. Por exemplo:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

y(t)=\sin \left(\theta (t,x)\right)=\sin(\omega t+kx)

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\frac {d\theta }{dx}}=k

Onde Número de onda, k, tem como unidade no SI radianos por metro (rad/m). No caso de mais do que uma dimensão espacial, número de onda é uma grandeza vetorial.

Ondas eletromagnéticas são normalmente descritas por qualquer uma das seguintes propriedades físicas: frequência (ƒ), comprimento de onda (λ), ou por energia de fóton (E). O comprimento de onda é inversamente proporcional a frequência da onda, a qual representa o números de períodos existentes na unidade de tempo.^[2] Desta forma, raios gama tem comprimentos do tamanho de frações do tamanho de um átomo, enquanto o comprimento de ondas no extremo oposto do espectro podem ser tão grandes quanto o universo. A energia de um fóton é diretamente proporcional à frequência de onda, portanto os raios gama possuem a maior energia, enquanto ondas de rádio possuem energias extremamente baixas.

Essas relações são ilustradas pelas seguintes equações:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

f={\frac {c}{\lambda }},\quad {\text{or}}\quad f={\frac {E}{h}},\quad {\text{or}}\quad E={\frac {hc}{\lambda }},

Onde:

c = 299792458 m/s é a velocidade da luz no vácuo e
h = 6.62606896(33)×10⁻³⁴ J s = 4.13566733(10)×10⁻¹⁵ eV s é a constante de Planck.

Pesquisar este blog

MECÂNICA GRACELI GENER. - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [800]

Teoria

Temperatura Unruh

Fórmula

Definições e unidades

Medição

Por estroboscópio

Métodos heteródinos

Frequência das ondas

Luz

Som

Frequências usadas em transmissões de televisão

Outros tipos de frequência

Comentários

Postar um comentário